 | |||||||
| August decorating a young lass with Celtic knot. |
THE O'CONNOR KNOT
For 10 years, my musical partner in the Blarney band, August O'Connor, lived and worked at Grace Cathedral in San Francisco as a reader, artist and designer of vestments. Then, moving to Santa Cruz, she led sweat lodges for many years on the Pacific coast. But by far August's favorite church is wild nature.
August, as a talented graphic artist, worked for a time as art editor of a local newspaper. She created logos that still adorn local businesses and sweatshirts. August is particularly fascinated by Celtic knots, teaching classes on how to design them, painting Celtic knots on body parts and incorporating them into decorative objects and tattoos.
After becoming acquainted with her work, I asked August to design for me a personal Celtic knot which I have been using for many years on my business cards and as a signature/chop on documents and correspondence. I call it “Nick's Knot” but this knot is more appropriately credited to its inventor.
 |
| Nick admiring the O'Connor Knot |
The O'Connor Knot (or AOC Knot) is a Celtic-style knot with seven crossings. Knot theorists have recognized seven distinct knots with seven crossings and I have often wondered which of these seven official knots represents my personal knot, a curiosity which could be satisfied by forming a rope into an AOC Knot, then successfully deforming that rope into one of the seven classic forms. My few attempts along these lines have so far resulted only in random tangles.
Then, just a few days ago, I ran across an article by David Richeson in "Quanta”, an online science magazine, entitled “Why Mathematicians Study Knots” which informed me of a better way to match my O'Connor Knot with a knot having some official name.
I learned from this article that knots played a brief role in physics at the end of the 19th century when William Thomson (Lord Kelvin) and P. W. Tait conjectured that atoms were formed of knots (vortex rings) tied in the electromagnetic ether.
Einstein's Theory of Special Relativity banished the ether which put an end to the knotty atom hypothesis. But P. W. Tait continued to be fascinated by knots, compiling long lists of knots with various crossing numbers, studying their properties and, in effect, turning himself into the world's first Knot Theorist. (See “The Knots of Peter Guthrie Tait.”)
Paying homage to Kelvin and Tait's failed theory of atoms, Quanta magazine published a table of all knots up to seven crossings in the style of the familiar Periodic Table of the Elements. This article also showed me an easy way to match Nick's Knot -- by calculating its mathematical knot invariants and comparing them with the knot invariants of the Magnificent Seven.
 |
| List of Knots in the form of Periodic Table |
So I proceeded to immerse myself in Knot Theory, mostly by watching videos on YouTube and by consulting the wonderful Atlas of Knots on the Web. Some of the knot invariants are easy to come by. The others require some simple but tedious graphing and calculation.
The first knot invariant is the Crossing Number which I already knew to be seven. The second is the Unknotting Number “u” which is the minimum number of eliminated crossings which will turn the knot into a simple loop (or “Unknot”). The third quantity is the Coloring Number “C” which is the minimum number of colors needed to color the knot segments under simple restraints.The Coloring Number, however is not an invariant. Coloring Number changes depending on how the knot is drawn, except in the case of C = 3, which is a true knot invariant, dividing all knots into two distinct classes depending on whether they are 3-colorable or not.
Incorporating these three quantities (and a fourth labeled “W”) I redrew the Quanta Knot Table including the unknown O'Connor Knot.
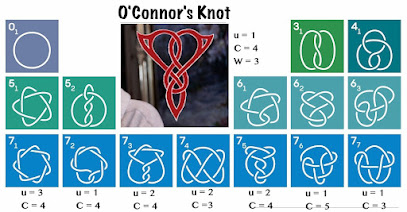 |
| What's the place of the stately O'Connor Knot? |
By trial and error, and using colored markers, I was able to determine the Unknotting Number u and the Coloring Number C of the AOC Knot. Unknotting Number of AOC is 1 and Coloring Number is 4. This last result means that the O'Connor Knot does not belong to the exclusive class of 3-colorable knots, which immediately eliminates knots 7(4) and 7(7) which do happen to be 3-colorable.
The only remaining candidate knots in the Periodic Table with u =1 are the knots 7(2) and 7(6) neither of which much resemble the AOC Knot in their official presentations. So further investigation is necessary to decide which of these two will be the winner in this knotty look-alike contest.
The knot 7(5), in this representation, seems to most closely resemble the AOC Knot, but that can't work because 7(5) has the wrong Unknotting Number.
Time to go to work. I formed an oriented AOC Knot and labeled each of its 7 crossings and each of its 7 segments according to a scheme devised by Princeton math professor James Waddell Alexander in 1928. My intent was to calculate the AOC Knot's Alexander Polynomial which is for knots a unique mathematical identity card.
In addition to his mathematical fame, Professor Alexander was a notable mountaineer in both Europe and the United States. A rock formation in the Colorado Rockies bears his name —Alexander's Chimney. While at Princeton, Alexander liked to climb university buildings, and always left his office window on the top floor of Fine Hall open so that he could enter by climbing the building.
i can confirm that using buildings for practice climbs is not confined to Princeton. While a graduate student at Stanford in the early Sixties, my office on the second floor of Inner Quad was adjacent to a radiator with a nylon rope attached. Physics students so inclined (not myself) would skip the stairs, toss the rope out the window and rappel directly down to campus.
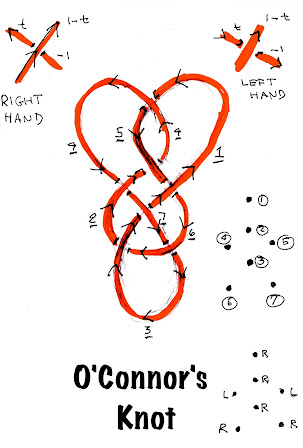 |
| The Oriented AOC Knot awaiting Alexanderization |
Alexander's genius was to discover a useful way to mathematicize the crossings and segments of a knot such that these numbers could be combined to uniquely characterize any knot no matter how complicated.
One of the features of Alexander's Way of looking at knots is that it divides all crossings into Right Crossings and Left Crossings. This division immediately gives rise to another simple knot constant — its “Writhing Number” (or simply its “Writhe”), a nomenclature I adore for its squirmy feeling.
A knot's Writhing Number “W” is defined as its number of Right-hand Crossings minus its number of Left-hand Crossings. The Writhing Number of the AOC Knot is 5 - 2 = 3.
All odd-crossing-numbered knots exist in two forms. The trefoil knot 3(1), for example, differs from its mirror image 3(1)*, a knot property called “chirality” or “handedness”. Trefoil knot 3(1) consists of three Right-hand Crossings (W = 3) while its mirror image 3(1)* is composed of three Left-hand Crossings (W = -3)
Since the handedness of a crossing does not change when the direction of its orientation arrows are reversed, it appears that handedness is a robust property of a knot diagram. When reflected in a mirror though, all RH crossing change into LH crossings and vice versa, so the Writhing Number will change sign under mirror reflection. Following this logic, the Writhing Number of the AOC Knot's mirror image would be W = -3.
Calculating the Writhing Numbers of the two candidate look-alikes we obtain W = 7 - 0 = 7 for J(2) and W = 5 - 2 = 3 for J(6). This result would seem to cinch the contest in favor of J(6) since both J(6) and the AOC Knot possess the same Writhe.
However I notice in the Atlas of Knots that the Writhing Number is not listed as one of the several parameters that distinguish one knot from its fellows. If the Writhing Number depends on how the knot is drawn then this conclusion that AOC Knot and the J(6) knot are the same might be false.The gold standard for separating one knot from another appears to be the Alexander Polynomial which can be computed from the former Crossing and Sector labeling scheme by forming the knot's Alexander Matrix, which in the case of the AOC Knot, looks like this:
From this matrix, a simple but tedious calculation (finding the determinant of a 6x6 matrix at least half of whose entries are zero) suffices to produce the desired Alexander Polynomial. It took me about an hour to generate the first result. which agreed with neither of the AP's listed for the two candidate knots. I repeated the calculation getting a different result. Still no match. (I have never been good at doing calculations involving loads of simple arithmatic where one wrong minus sign can shipwreck the entire crew. This is the kind of mindless arithmatic for which computers were invented.) I confess that I did this stupid calculation 12 times and got 12 different answers, each time though correcting at least one error in my previous work. This task consumed three days and lots of paper.
Then on the morning of the fourth day of boring high-school level arithmatic, I fixed my final mistake. And managed to calculate my first real Alexander Polynomial!
The same Alexander Polynomial listed in the Knot Atlas for J(6).
This agreement of the two knot's Alexander Polynomials means that despite their superficial differences, the AOC Knot and the J(6) Knot are exactly the same knot. Also they are not mirror images because their Writhing Numbers are identical. (One weakness of the Alexander Polynomial is that it does not distinguish between a knot and its mirror image.)
In real life I have not yet been able to deform my AOC Knot rope into a J(6) Knot rope but my four-day pilgrimage into Knot Land has blessed me with the certainty that such a deformation is surely possible.
August continues to produce original sketches of lively animals, to hammer out odd copper orbitals and to create beautiful Celtic knots. One of my favorites is her “Love Knot” formed with 11 alternating crossings. The Knot Encyclopedia lists 367 different alternating 11-crossing knots. The Writhing Number of O'Connor's Love Knot happens to be 7 - 4 = 3, the same Writhing Number as her AOC Knot. And so we come back to where this knotty inquiry first began.
 |
| August O'Connor's "Love Knot" |



4 comments:
bravo Nick
Thanks Nick for a lovely reminder of August all these years later
Wowza, Nick!
I always knew you were naughty but this is next level Knotty!! Bravo! 👏🥰😘
Diana
August is recalling, Malcolm, your telling us at Britannia of your times in the mines, and the fine music sessions at your little castle in Boulder Creek
Post a Comment