The O'Connor Knot

August decorating a young lass with Celtic knot.

THE O'CONNOR KNOT

For 10 years, my musical partner in the Blarney band, August O'Connor, lived and worked at Grace Cathedral in San Francisco as a reader, artist and designer of vestments. Then, moving to Santa Cruz, she led sweat lodges for many years on the Pacific coast. But by far August's favorite church is wild nature.

August, as a talented graphic artist, worked for a time as art editor of a local newspaper. She created logos that still adorn local businesses and sweatshirts. August is particularly fascinated by Celtic knots, teaching classes on how to design them, painting Celtic knots on body parts and incorporating them into decorative objects and tattoos.

After becoming acquainted with her work, I asked August to design for me a personal Celtic knot which I have been using for many years on my business cards and as a signature/chop on documents and correspondence. I call it “Nick's Knot” but this knot is more appropriately credited to its inventor. 

Nick admiring the O'Connor Knot

The O'Connor Knot (or AOC Knot) is a Celtic-style knot with seven crossings. Knot theorists have recognized seven distinct knots with seven crossings and I have often wondered which of these seven official knots represents my personal knot, a curiosity which could be satisfied by forming a rope into an AOC Knot, then successfully deforming that rope into one of the seven classic forms. My few attempts along these lines have so far resulted only in random tangles.

Then, just a few days ago, I ran across an article by David Richeson in "Quanta”, an online science magazine, entitled “Why Mathematicians Study Knots” which informed me of a better way to match my O'Connor Knot with a knot having some official name.

I learned from this article that knots played a brief role in physics at the end of the 19th century when William Thomson (Lord Kelvin) and P. W. Tait conjectured that atoms were formed of knots (vortex rings) tied in the electromagnetic ether.

Einstein's Theory of Special Relativity banished the ether which put an end to the knotty atom hypothesis. But P. W. Tait continued to be fascinated by knots, compiling long lists of knots with various crossing numbers, studying their properties and, in effect, turning himself into the world's first Knot Theorist. (See “The Knots of Peter Guthrie Tait.”)

Paying homage to Kelvin and Tait's failed theory of atoms, Quanta magazine published a table of all knots up to seven crossings in the style of the familiar Periodic Table of the Elements. This article also showed me an easy way to match Nick's Knot -- by calculating its mathematical knot invariants and comparing them with the knot invariants of the Magnificent Seven.

List of Knots in the form of Periodic Table

So I proceeded to immerse myself in Knot Theory, mostly by watching videos on YouTube and by consulting the wonderful Atlas of Knots on the Web. Some of the knot invariants are easy to come by. The others require some simple but tedious graphing and calculation.

The first knot invariant is the Crossing Number which I already knew to be seven. The second is the Unknotting Number “u” which is the minimum number of eliminated crossings which will turn the knot into a simple loop (or “Unknot”). The third quantity is the Coloring Number “C” which is the minimum number of colors needed to color the knot segments under simple restraints.The Coloring Number, however is not an invariant. Coloring Number changes depending on how the knot is drawn, except in the case of C = 3, which is a true knot invariant, dividing all knots into two distinct classes depending on whether they are 3-colorable or not.

Incorporating these three quantities (and a fourth labeled “W”) I redrew the Quanta Knot Table including the unknown O'Connor Knot. 

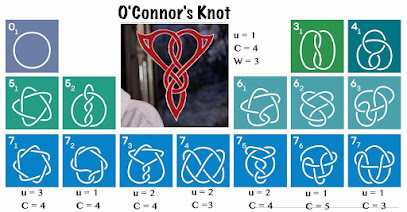What's the place of the stately O'Connor Knot?

By trial and error, and using colored markers, I was able to determine the Unknotting Number u and the Coloring Number C of the AOC Knot. Unknotting Number of AOC is 1 and Coloring Number is 4. This last result means that the O'Connor Knot does not belong to the exclusive class of 3-colorable knots, which immediately eliminates knots 7(4) and 7(7) which do happen to be 3-colorable.

The only remaining candidate knots in the Periodic Table with u =1 are the knots 7(2) and 7(6) neither of which much resemble the AOC Knot in their official presentations. So further investigation is necessary to decide which of these two will be the winner in this knotty look-alike contest.

The knot 7(5), in this representation, seems to most closely resemble the AOC Knot, but that can't work because 7(5) has the wrong Unknotting Number.

Time to go to work. I formed an oriented AOC Knot and labeled each of its 7 crossings and each of its 7 segments according to a scheme devised by Princeton math professor James Waddell Alexander in 1928. My intent was to calculate the AOC Knot's Alexander Polynomial which is for knots a unique mathematical identity card.

In addition to his mathematical fame, Professor Alexander was a notable mountaineer in both Europe and the United States. A rock formation in the Colorado Rockies bears his name —Alexander's Chimney. While at Princeton, Alexander liked to climb university buildings, and always left his office window on the top floor of Fine Hall open so that he could enter by climbing the building. 

i can confirm that using buildings for practice climbs is not confined to Princeton. While a graduate student at Stanford in the early Sixties, my office on the second floor of Inner Quad was adjacent to a radiator with a nylon rope attached. Physics students so inclined (not myself) would skip the stairs, toss the rope out the window and rappel directly down to campus. 

The Oriented AOC Knot awaiting Alexanderization

Alexander's genius was to discover a useful way to mathematicize the crossings and segments of a knot such that these numbers could be combined to uniquely characterize any knot no matter how complicated.

One of the features of Alexander's Way of looking at knots is that it divides all crossings into Right Crossings and Left Crossings. This division immediately gives rise to another simple knot constant — its “Writhing Number” (or simply its “Writhe”), a nomenclature I adore for its squirmy feeling.

A knot's Writhing Number “W” is defined as its number of Right-hand Crossings minus its number of Left-hand Crossings. The Writhing Number of the AOC Knot is 5 - 2 = 3.

All odd-crossing-numbered knots exist in two forms. The trefoil knot 3(1), for example, differs from its mirror image 3(1)*, a knot property called “chirality” or “handedness”. Trefoil knot 3(1) consists of three Right-hand Crossings (W = 3) while its mirror image 3(1)* is composed of three Left-hand Crossings (W = -3)

Since the handedness of a crossing does not change when the direction of its orientation arrows are reversed, it appears that handedness is a robust property of a knot diagram. When reflected in a mirror though, all RH crossing change into LH crossings and vice versa, so the Writhing Number will change sign under mirror reflection. Following this logic, the Writhing Number of the AOC Knot's mirror image would be W = -3.

Calculating the Writhing Numbers of the two candidate look-alikes we obtain W = 7 - 0 = 7 for J(2) and W = 5 - 2 = 3 for J(6). This result would seem to cinch the contest in favor of J(6) since both J(6) and the AOC Knot possess the same Writhe.

However I notice in the Atlas of Knots that the Writhing Number is not listed as one of the several parameters that distinguish one knot from its fellows. If the Writhing Number depends on how the knot is drawn then this conclusion that AOC Knot and the J(6) knot are the same might be false.The gold standard for separating one knot from another appears to be the Alexander Polynomial which can be computed from the former Crossing and Sector labeling scheme by forming the knot's Alexander Matrix, which in the case of the AOC Knot, looks like this: 

From this matrix, a simple but tedious calculation (finding the determinant of a 6x6 matrix at least half of whose entries are zero) suffices to produce the desired Alexander Polynomial. It took me about an hour to generate the first result. which agreed with neither of the AP's listed for the two candidate knots. I repeated the calculation getting a different result. Still no match. (I have never been good at doing calculations involving loads of simple arithmatic where one wrong minus sign can shipwreck the entire crew. This is the kind of mindless arithmatic for which computers were invented.) I confess that I did this stupid calculation 12 times and got 12 different answers, each time though correcting at least one error in my previous work. This task consumed three days and lots of paper.

Then on the morning of the fourth day of boring high-school level arithmatic, I fixed my final mistake. And managed to calculate my first real Alexander Polynomial!

The same Alexander Polynomial listed in the Knot Atlas for J(6).

This agreement of the two knot's Alexander Polynomials means that despite their superficial differences, the AOC Knot and the J(6) Knot are exactly the same knot. Also they are not mirror images because their Writhing Numbers are identical. (One weakness of the Alexander Polynomial is that it does not distinguish between a knot and its mirror image.)

In real life I have not yet been able to deform my AOC Knot rope into a J(6) Knot rope but my four-day pilgrimage into Knot Land has blessed me with the certainty that such a deformation is surely possible.

August continues to produce original sketches of lively animals, to hammer out odd copper orbitals and to create beautiful Celtic knots. One of my favorites is her “Love Knot” formed with 11 alternating crossings. The Knot Encyclopedia lists 367 different alternating 11-crossing knots. The Writhing Number of O'Connor's Love Knot happens to be 7 - 4 = 3, the same Writhing Number as her AOC Knot. And so we come back to where this knotty inquiry first began. 

August O'Connor's "Love Knot"

A New Kind of Saint

November 1: All Saints Day

A NEW KIND OF SAINT

In this Age that couldn't be Darker

When the Lamp of Wisdom grows faint

When the Empire of Lies seems to triumph

We are needing a new kind of saint.

 

A saint who comes out of nowhere

From a direction you'd never expect

A saint who's tantric, organic and quantum

And politically incorrect.

 

A saint that performs needful miracles

More beautiful and bigger than most

Not by him but through him manifested

By the grace of a new Holy Ghost. 

Might not be a Hindu or Buddhist

Nor a Protestant, Catholic or Jew

Nor even a bright quantum physicist

Could even be me or be you.

Could even be you, my friend

When you say yes to that calling inside you.

Reality on Radio

THE DOCTOR FUTURE SHOW
KSCO, SANTA CRUZ, CA 1080AM

Interview - Physicist Nick Herbert on the latest Nobel Physics Prize on Bell's Theorem, Quantum Entanglement, and Non-local Reality

http://www.drfutureshow.com/?fbclid=IwAR14sVgx7HbfCseEzkKYkI1DXTPCS6XBZJg-7fhx-fsBZzUVXdWNjLMul3A&mibextid=34ey5e

Or

http://futurepeak.net/audio/DrF604_20221011_NickHerbert.mp3 

Quantum physicist Nick Herbert is our special guest for the full two hours of today's show, speaking about the latest Nobel Physics Prize on Bell's Theorem, Quantum Entanglement, and Non-local Reality. He and John Clauser, one of this  year's awardees of the prestigious prize, were colleagues together in the Fundamental Fysiks Group back in the 1970's, when this line of research was being explored.

Nick makes the point that Bell's Theorem was ignored back in 1964, when it was first espoused, not because it was bad science, but because it was looking at Reality, not theory, and physicists at the time considered Reality out-of-bounds for physics research.

 So today we'll be taking a fresh look at John Bell's work, faster-than-light signaling, quantum encryption, quantum teleportation, making entangled photons, quantum computers, creating reality with our thoughts, and wondering whether consciousness is our reward for...'collapsing the wave function'?!! Enjoy!

The Reality Prize

Esalen Seminar on the Nature of Reality Poster

THE REALITY PRIZE

 In the late 1970s, Esalen Institute co-founder Michael Murphy decided to invite physicists down to Big Sur to see what might happen. One of Mike's speculations was that “Perhaps a new kind of inspired physicist, experienced in the yogic modes of perception, might emerge to comprehend the further reaches of matter, space and time.” So it happened that physicist Saul-Paul Sirag and myself found ourselves leading workshops on quantum mechanics for Esalen guests and holding yearly invitational conferences for selected scientists focused mainly on the theme of Irish physicist John Stewart Bell's non-locality theorem for quantum-entangled systems.

Quantum theory is one of our most successful mathematical tools for understanding the behavior of Nature at her most basic level. This theory has never made a wrong prediction and some of its results agree with experiment up to 13 decimal places. However its success is marred by what one might call The Reality Crisis. Though I have struggled with this theory for more than fifty years, I cannot tell my son Khola a simple story about how the world works on the quantum level. And neither can anyone else.

Quantum physicists represent the world in two ways depending on whether the world's being looked at or not. Waves of possibility when not looked at; And an actual particle when we look. Plus physicists don't really know what “looking” means — an embarrassing situation called “the measurement problem”. Wanna stump a physicist? Ask him (or her) what they think it takes to turn many shimmering quantum possibilities into one hard quantum fact.

Oddly enough, The Reality Crisis (physicist's inability to tell a good quantum story) does not hamper at all our ability to use this wonderful tool to make successful predictions. So, for the most part, practical physicists have consigned “thinking about reality” to the philosophers, to physicists who have already made their mark in the world and to amateurs (from the French word “to love”) who have no reputation to lose. “Do not keep saying to yourself if you can possibly avoid it,” warned physicist Richard Feynman, 'But how can it be like that?' because you will go 'down the drain' into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that.”

To explain how one particle becomes actual is puzzling enough, but the stakes are raised once two particles are involved, especially if they happen to be created in a state of “quantum entanglement”. Then, when unlooked at at least, the two entities do not possess their own attributes. Only the union of the two is in a definite state of being, until a measurement is made. Erwin Schrōdinger was the first to point out the peculiar nature of entangled quantum systems and to comment that this strange mode of being was what most distinguished the quantum world from everyday stuff..

But in Schrōdinger's day, entangled quantum systems were hard to come by. So quantum entanglement, for the most part, remained a theoretical curiosity, if it was even mentioned at all.

That all changed in 1964, when a physicist named John Stewart Bell, whose hobby happened to be quantum reality, discovered, during a sabbatical leave from his day job at CERN accelerator, what is now know as “Bell's Theorem.”

The Bell Experiment

 

Imagine a source S of polarization-entangled photon pairs A and B. Photon A is sent to Alice and photon B to Bob who each have a device that measures photon polarization. One of the important features of a quantum measurement is that Alice cannot just ask “what properties does her A photon actually possess?” but must make a choice of what attribute to ask about and which attributes to leave unknown.

Quantum attributes come in complementary pairs (and often triplets). If you ask about position, you forego finding out about momentum, a discovery attributed to Heisenberg, known as “the uncertainty principle”. Photon polarization happens to be one of those quantum attributes that is triplely uncertain, so when Alice chooses to measure one photon polarization plane, she necessarily forfeits all knowledge of the other two polarization planes.

At both Alice and Bob's stations, imagine a clock face that represents the direction that the two experimenters choose to interrogate their photon's unknown polarization. If Alice chooses to ask at 12 o'clock, a PLUS in her detector means that her A photon polarization is Vertical (V); a MINUS means that its polarization is Horizontal (H).

Two features of this system are typical of an entangled state:. 1. No matter what their clock settings, each observer always gets a random sequence of PLUSs and MINUSs; 2. Whenever Alice's setting is the same as Bob's, if Alice gets a PLUS, Bob will always get a MINUS and vice versa. Their results are said to be 1. Perfectly random and 2. Perfectly anti-correlated.

Since polarization-entangled states were almost non-existent in 1964, nobody really knew if this would actually happen to Alice and Bob, but a simple quantum calculation gives the result quoted above.

Physicists “represent” an unobserved quantum system by a mathematical entity called a wavefunction. I carefully use the word “represent” rather than “describe” because we don't really know what the real relationship is between the wavefunction and the actual world, another embarrassing situation called “the interpretation problem”. Physicists know how to use the wavefunction to correctly calculate (the probability of) all experimental results but they don't really know what the wavefunction means.

So what more does this magnificently useful but utterly mysterious wavefunction say about the Alice and Bob experiment?

First: Quantum theory says that whatever happens is entirely independent of the distance between Alice and Bob. If they are in the same room, as in most practical physics experiments, the results will be exactly the same as if they were ten thousand light years apart, separated by vast interstellar distances.

Second: While unobserved, the wavefunction does not assign any polarization attribute to either Alice's or Bob's photon, but when Alice measures her photon, using a clock direction of her choice, her photon instantly acquires a definite value, AND SO DOES BOB'S PHOTON even though Alice and Bob might be separated by galactic distance. This instantaneous connection, if it is real and not just confined to the theory, violates all the norms of modern physics.

Alice's apparently instant action on Bob's photon has gotta be faster than light (goodbye Einstein) but that's only part of the trouble. This interaction, unlike any we are familiar with in physics, is not diminished by distance. Furthermore, this Alice-Bob intimacy is not transmitted by any field we know of-- it just happens. Alice's action on Bob's photon is, in brief, unmitigated, unmediated and immediate.

Physicists label such alleged behavior, as “non-local”, a tame word that conceals their deep intellectual loathing for an unholy abomination, for a deeply unnatural act. In the world of physics, a “non-local interaction¨, if such a thing ever occured, would be a mortal sin against the Holy Ghost. Non-local interactions are, in physicist's minds, comparable to believing in voodoo, which, come to think of it, is alleged by its practitioners to behave somewhat “non-locally” too.

Third: But what about Einstein? If Alice has access to a non-local interaction, can she and Bob exchange signals faster than light using entangled photons? Since quantum theory describes all experiments perfectly, it can easily answer this question. And the answer is NO. No superluminal signaling is possible using entangled photons. What forbids this is the randomness of each individual event which exactly smothers any alleged non-local Alice-Bob connection.

So what did Bell do with this strange situation? He went against Feynman’s warning about trying to tell a story about what's really going on. Bell's Theorem is not about quantum THEORY, not about quantum EXPERIMENTS, but about quantum REALITY.

Bell tried to imagine the most general model of reality that he could think of, using the term “hidden variables” to make his guesses amenable to mathematical calculation. He imagined all the influences that might go into forming Bob's polarization measurement and left out just one: Alice's choice of what to measure. If Alice's choice is allowed to influence Bob's result, that would imply the existence of a real (we're talking about reality here) non-local interaction in Nature.

Using this one assumption, Bell calculated a set of inequalities that the EXPERIMENTAL RESULTS of any local model of reality must satisfy.

Guess what? The results predicted by quantum mechanics do not obey the Bell Inequalities. Therefore REALITY MUST BE NON-LOCAL. Bring out your crosses and holy waters, folks. The witch doctors is loose!

The reception of Bell's remarkable proof, which was published in 1964, in an obscure and rather short-lived journal, was a resounding silence. John Clauser, then a graduate student at Columbia, discovered Bell's Theorem in 1969 and wrote him about the possibility of doing an actual experiment to check whether the quantum predictions were correct. Bell reported that this was the first comment on his paper he had yet received—more than four years after its publication.

You often hear it said that when Albert Einstein published his Special Theory of Relativity,  only six people understood it. In truth, there were probably lots more than six. But it is fair to say, that when John Bell published his now famous paper, ONLY SIX PEOPLE CARED. John Clauser was one of them.

For the next part of the story I quote David Kaiser's “How the Hippies Saved Physics” which discusses Clauser's accomplishments in great detail.

“Clauser, a budding experimentalist, realized that Bell's theorem could be amenable to real-world tests in a laboratory. Excited, he told his thesis advisor about his find, only to be rebuffed for wasting their time on such philosophical questions. Soon Clauser would be kicked out of some of the finest offices in physics, from Robert Serber's at Columbia to Richard Feynman's at Caltech. Bowing to these pressures, Clauser pursued a dissertation on a more acceptable topic—radio astronomy and astrophysics—but in the back of his mind he continued to puzzle through how Bell's inequality might be put to the test.”

John Clauser lecturing at Esalen

 I first met John Clauser in his lab at Berkeley in the early 70s where he had cobbled together an ingenious device to test the Bell Inequalities using the few entangled photons that a mercury-vapor lamp produces. He hoped he would gain fame by showing that, for this particular system, quantum theory was wrong, and Reality was Local, as Einstein would have guessed. He succeeded however in finding that quantum theory was right, which means, according to Bell's Proof, that Reality must be non-local! This world, all that we can see around us, remains stubbornly local, but is undergirded, at least in the case of entangled photons, by a network of instant invisible voodoo-like connections.

I was introduced to Clauser as a member of Elizabeth Rauscher and George Weissman's Fundamental Fysiks Group and marveled at his Rube Goldberg setup for measuring polarized-photon coincidences. (He was using pile-of-plates polarizers, for Gods sake!) In addition to recruiting experimentalist John Clauser, FFG also attracted Henry Pierce Stapp, a Berkeley theorist interested in fundamental questions. All of our later ESNR meetings included Clauser and Stapp as core personnel.

Henry Stapp pushed us to closely examine every assumption that goes into Bell's proof, especially those that seem most self-evident, and Clauser kept us posted on other Bell Inequality tests besides his own that were being planned and carried out around the world.

The title of our Esalen Conference: Esalen Seminars on the Nature of Reality, was neither silly nor pretentious. We really were studying “reality” as physicists might view it, as an attempt to tell a story about what's actually going on behind the wavefunction mystery and the measurement mystery. For our ESNR motto we chose a quote from Goethe's Faust, who was also a passionate seeker of Reality. Attesting to the real strangeness of our quest, Clauser's colleague Abner Shimony dubbed these Bell tests "experimental metaphysics."

Our third Esalen meeting (ESNR #3) in 1982 featured a ceremony sponsored by Charles Brandon, one of the founders of Federal Express, to award both John Bell and John Clauser “The Reality Prize” of $3000 each for their firm establishment through theory and experiment of non-locality as a general feature of the world. Bell's Reality Prize was accepted by French physicist Bernard d'Espagnat since Bell could not be there in person. We assured the participants that this prize was merely the first of many that would be bestowed upon the two of them.

Reality Prize Announcement: Esalen Catalog

 

Unfortunately, John Stewart Bell died in 1990, at the age of 62 of a cerebral hemorrhage.

In 2010, John Clauser, Alain Aspect and Anton Zeilinger were awarded the prestigious (Ricardo) Wolf Prize.

And just last week, the same three men were honored with the 2022 Nobel Prize in Physics.

Hearty congratulations to all three of you, O bold and noble champions of quantum reality!

Clauser, Zeilinger, Aspect: Physics Nobel Prize 2022: Quanta Magazine

108 Chakra Rosary (Version Two)

108 Chakra Rosary (Version Two)

108 CHAKRA ROSARY (VERSION TWO)

Recently Nick developed a system of 108 Chakras (body parts that can be accessed by mind) and a systematic way of exploring these parts in a particular sequence (108 Chakra Rosary). The easiest way to construct such a rosary would be as a loop of 108 beads, as in traditional Buddhist malas. Too many beads I thought. And so I developed a more compact rosary consisting of only 32 beads. But what this small rosary gains in compactness, it loses in the complicated instructions concerning how to fit 108 body parts into 32 beads.

 

After playing with the original instruction set, I have recently revised the counting of the 108 chakras using 32 beads in this second version which seems to me more natural and easier to remember than the first.

Compact 108 Chakra Rosary

This compact 108 chakra rosary consists of an outer loop of 24 beads, half of them dark and half lite corresponding to my division of chakras into dark and lite, the dark chakras located primarily in the lower parts of the body and the lite chakras situated on top. This outer loop is mostly used to count the 48 Limb Chakras--the 24 Right Limbs circling the loop in CW (Clockwise) direction and the 24  Left Limbs circling in CCW (CounterClockwise) direction. This outer loop is bisected by a string of 8 rainbow beads which are used to count the five 8-chakras sets: Spinal, Hindu, Sensual, Pelvic and Rib-Cage Chakras. The outer loop is also used to count the 18 Cranial Chakras.

In the center of the lite beads is a LITE link which attaches to a Lite Disk on which the rosary begins. In the center of the dark beads is a DARK link which attaches to a Dark Disk on which the rosary ends. Two other compact rosary landmarks are the TOP link and BTM link on which the 8-chakra sequences start and end.

Intro or Antiphon Move

Move #0: Starting at the Lite Disk, move onto the LITE link and follow the 6 lite beads to the TOP link. These six beads are merely an excuse to move to the TOP link where the rosary proper begins.  Counting these first beads is the time to formulate why you are focusing your attention on your body's Somatic Stations, whether out of curiosity, exploration, gratitude, meditation or just to practice the moves. These six beads correspond roughly to the Antiphon beads of a Catholic rosary.

Move #1:  24 Right Limb Chakras

 Move #1: 24 Right Limb Chakras. The chakra rosary proper starts at the TOP link and begins with the RIGHT FOOT chakra. Moving Clockwise (CW) around the outer beads, touching all 24 beads and returning to the TOP link. Each of the four chakra symbols: Right Foot, Right Leg, Right Arm and Right Hand represent six chakras. An example of dark/lite symmetry: the Right Hand Chakra is the lite partner to the dark Right Foot Chakra; The Right Arm Chakra is the lite partner to the dark Right Leg Chakra.

Beginning on the first six dark beads: 

1, Right Foot, 2. Big Toe 3. Two Toe.

    

4. Three Toe, 5. Four Toe, 6. Five Toe.

 

As an aid to memorization, the Limb Chakras are counted in groups of three (as are the 18 Cranial Chakras) while the rest of the chakras are counted in groups of two.

 

 7. Ankle,  8. Calf,  9. Knee.

                

10. Thigh, 11. Hip Joint, 12. Right Leg.

 

13 Right Arm, 14. Shoulder Joint, 15. Upper Arm.

               

16. Elbow, 17. Forearm, 18. Wrist.

19. Five Finger,  20. Four Finger,  21. Three Finger.  

22. Two Finger,  23. Thumb,  24. Right Hand.

The purpose of the chakra rosary is to focus your attention on otherwise neglected body parts. It is not a speed contest, although you may want to pay attention to some parts more than others. "Pay attention" -- an unusual phrase: the monetization of consciousness?

Move #2: 8 Spinal Chakras

Move #2: 8 Spinal Chakras. Beginning at the TOP link, move down the 8 rainbow beads, counting the chakras in Lite/Dark groups of two, each lite chakra paired with its dark partner.

 25, Will,       26. Auto    

27. Neck,       28. Tail        

29. Thorax,    30. Pelvis.            

 31. Lumbar,   32. Perineum. 

Where here Will stands for the voluntary nervous system, some of whose plexuses are located along the spine. And Auto represents the Involuntary nervous system to which strictly speaking you cannot really focus your attention. However on this Auto bead one can contemplate the importance of our unconscious bodily operations and give them some appreciation..

Although we humans do not possess tails, the Neck/Tail pairing associates the cervical vertebrae with the coccyx (or tailbone).

The Lumbar is paired with the Perineum because both are saddle-shaped. 

Move #3: 8 Hindu Chakras

 Move #3: 8 Hindu Chakras. These are my own variations on the seven classic Hindu chakras. The major changes are the addition of an eighth chakra (named Ground) so that the Dark/Lite pairing could be preserved. Also I invented simple traffic-sign-like symbols to replace the classic many-petaled lotus designs.

Starting at the BTM link and moving up the rainbow beads in Dark/Lite pairs we go:          

33. Ground,   34. Crown               

35. Root,        36. Brow                                                              

37. Sex,          38. Throat                      

 39. Belly,       40. Heart.

I invented the new (dark) Ground Chakra as a partner to the classic (lite) Crown Chakra. The Ground Chakra represents our connection with the Earth and is located at the soles of the (bare) feet; the lite Crown Chakra represents our connection with Divinity and is situated at the top of the head. The dark circle symbolizing Ground could be the Moon or the Fertile Darkness; the lite circle symbolizing Crown could be the Sun or Cosmic Enlightenment.

The dark Root Chakra stands for Security, a solid place to sit; the lite Brow Chakra represents the Mind, or psychic powers. The symbol for the dark Root Chakra could be a plus sign --what is more basic than arithmetic?--or it could represent the anus, also called the fundament. The symbol for the lite (mind) Brow Chakra could represent the unknown quantity X or the Third Eye.

The vertical stroke in the dark Sex Chakra could represent either lingam or yoni; the horizontal stroke in its corresponding lite Throat Chakra could stand for either the vocal chords or the lips through which the voice emerges.

The dark Belly Chakra represents the center of gravity, the hara of Japanese martial arts. the lite Heart Chakra represents the body's feeling center, the hara of your emotional body.

Move #4: 8 Sensual Chakras

 Move #4: 8 Sensual Chakras. These are eight ways your body interacts with the outside world.

Starting at TOP link we count down the rainbow beads in Lite/Dark pairs.

 41. Eyes,    42. Ears                  

43. Nose,     44. Skin           

45. Mouth,   46. Tongue          

47. Lungs,    48. Bowels.

Note that the symbols for the Lite/Dark Chakra pair Nose/Skin are both two dots. The two Nose dots represent the nostrils and the two Skin dots represent the armpits.

Move #5: 24 Left Limb Chakras

 

Move #5: 24 Left Limb Chakras. Like the Right Limb Chakras, the 24 Left Limb Chakras are counted on the 24 outer beads but this time, starting at BTM link, the beads are encircled in the opposite direction --CCW (CounterClockwise) starting with the LEFT FOOT CHAKRA and counting in threes.

 49. Left Foot,  50. Big Toe,  51.Two Toe.                               52. Three Toe, 53. Four Toe, 54. Five Toe

55. Ankle, 56. Calf,  57. Knee.                                                58. Thigh, 59. Hip Joint, 60. Left Leg.

61, Right Arm, 62. Right Shoulder Joint, 63. Upper Arm.      64. Elbow, 65. Forearm, 66. Wrist

 67. Five Finger, 68. Four Finger, 69. Three Finger.               70, Two Finger, 71. Thumb,  72. Left Hand.

Move #6: 8 Pelvic & 8 Rib-cage Chakras

 

After visiting 72 chakras, we next enter the realm of the Three Bony Containers: 1. the Pelvic Basin, 2. the Rib Cage and 3. the Skull.

Move #6: 8 Pelvic & 8 Rib-cage Chakras. Starting at the BTM link we ascend the 8 rainbow beads in pairs. The Pelvic Chakras are all-Dark but we do not pair them here with their corresponding all-Lite Rib Cage Chakras.

73. Pelvic Basin,          74, Sacrum

75. Right Sitz Bone,     76. Left Sitz Bone

77. Right Pubic Bone,    78. Left Pubic Bone

79. Right Pelvic Bone,   80. Left Pelvic Bone.

Ending at the TOP link we now descend the 8 rainbow beads to BTM link

81. Right Rib Bones,     82. Left Rib Bones

83. Right Clavicle,        84. Left Clavicle

85. Right Scapula,         86, Left Scapula

87. Sternum,                 88. Rib Cage. 

Paying attention to only these 16 bones, you might notice that the Rib Cage resembles an upside-down Pelvic Basin.

Move #7: 18 Skull Chakras

Move #7: 18 Skull Chakras. Starting at BTM link, we ascend the outer lite beads in groups of three, two Right & Left paired lite Chakras plus a single dark Chakra:

89. Right Cheek Bone      90. Left Cheek Bone    91. Maxilla

92. Right Frontal Bone     93. Left Frontal Bone   94. Chin

 

95. Right Parietal Bone     96. Left Parietal Bone  

97. Mandible

 

98. Right Occipital Bone   99. Left Occipital Bone   

100. Inion

 

101, Right TM Joint         102. Left TM Joint       

103. Foramen

 

104. Right Temporal Bone  105. Left Temporal Bone  

106. Skull

 

Visiting these 18 Skull Chakras brings us to the DARK link where we finish off the 108 chakra rosary.

 

Move #8: Whole-Body and No-Body Chakras

 

 Move #8: Whole-Body and No-Body Chakras. Move from the DARK kink to the Dark Disk which represents the Whole-Body Chakra, paying attention to your body as a whole. Putting the rosary away or concealing it in one hand represents the No-Body Chakra, the whole Universe with a you-shaped hole cut out of it. Now expand your attention as best you can to fill the entire Cosmos.

A Rosary For 108 Chakras

A ROSARY FOR 108 CHAKRAS

One of the most important powers we possess is the ability to put our attention anywhere we please. In particular we can move our attention to any part of the body. A body part attended to is different from a body part ignored. A body part attended to "lights up" in a particular way.

To aid us in performing this mindful illumination of the body, I have been working for many years to increase the number of chakras (special body sites) from the classical seven Hindu chakras to a new and final total of one hundred and eight. Analogous to the particle/antiparticle symmetry of ordinary matter, I have applied a rough dark/light symmetry to my chakras. Each "light" chakra possesses a corresponding "dark" partner. In general (but not always) the dark chakra is located lower in the body than its homologous light partner. I have also tried to devise symbols "as simple as traffic signs" to represent both the classic chakras and my numerous additions.

Nick's new system consists of 108 locations in the body into which you can place your awareness and "see what happens". (Some of these places may already be clamoring for your attention by being painful.) See  Which of Your Body Parts Needs More Amour for more details of this system.

Once having designated these bodily locations, I wanted to invent a systematic way of touring them. There are thousands of possible tours (actually 108! = 108 factorial which my computer informs me is a number with 175 digits.) So the particular body tour I have chosen is certainly not unique but for me it seems to possess a certain logic that makes it easy to remember.

Most of the chakras fit into one of three groups: Limb Chakras, Central Chakras and the Bony Containers

1. The 4 Limb Chakras:

Right Leg:Foot Chakras (12)

Right Arm:Hand Chakras (12) 

Left Leg:Foot Chakras (12)

Left Arm:Hand Chakras (12)

For a total of 4 x 12 = 48 Limb chakras. (The underline indicates that all these chakras are "dark" Compare for instance, the "dark" Foot Chakras with the "light" Hand Chakras.)

2. The 3 Central Chakras:

Hindu Chakras (8)

Spinal Chakras (8)

Portal Chakras (8) (formerly called "Sensual Chakras")

For a total of 3 x 8 = 24 Central Chakras. Each dark Central chakra is paired with a light Central chakra. I am using the convention that upper-case "Chakra" refers to a group of body parts while lower-case "chakra" refers to one specific site. For example, the classic Hindu Chakras are eight in number, including the famous ("light") Heart chakra, whose "dark" partner is the Belly chakra.

3. The 3 Bony Containers

Pelvic Basin Chakras (8)

Rib Cage Chakras (8)

Skull Chakras (18) 

For a total of 8 + 8 + 18 = 34 Bony Container Chakras.

To these 106 main chakras  must be added a final two: the Whole Body chakra and the No Body chakra. The No Body chakra represents the entire Universe minus a tiny you-shaped piece. This final chakra stands for everything that is not your body, a distinction, which, as Alan Watts reminds us, may not be that easy to make: where exactly does your body end and the external Universe begin?

NICK'S BASIC 108 CHAKRA ROSARY

The simplest 108 chakra rosary would consist of 108 beads, each bead in the form of or depicting one of the chakra symbols shown above. Such a rosary would be large and difficult to produce. (Although the task might be made easier with the use of a 3D printer.) For my own purposes I have designed a smaller rosary consisting of only 32 beads. Nick's 32-bead rosary is more compact than the simplest rosary but explaining how to use it to visit all 108 chakras is more complicated.

Nick's Basic Chakra Rosary is made of 12 Light beads, 12 Dark beads and eight Rainbow beads plus a Light Disk and a Dark Disk which mark the beginning and end of "saying the Chakra Rosary". (In this photo, bad lighting unfortunately makes the Light Disk appear Dark and vice versa.)

As a rough guide to saying Nick's Chakra Rosary, the Light and Dark beads are used to "say" the Limb Chakras which come in groups of sixes, while the Rainbow beads are used to "say" the Central and Bony Container Chakras which come in groups of eight. (The eighteen Skull Chakras are the only exception to this rule.)

Another peculiarity of this system is that except for the Central Chakras, most of the saying of the beads follows an obvious anatomical sequence. In the case of the three Central Chakras, however, the saying of the beads alternates between a Dark chakra and a Light chakra following only a rough anatomical sequence.

THE SAYING OF THE BASIC CHAKRA ROSARY BEADS

We publish here the first account of the saying of the Basic Rosary beads. Holding the rosary as shown above, with the Light beads on the left and the Rainbow beads oriented with the single Light bead at the top, the sequence begins on the Light Disk. As your fingers move down the six white beads, this is the time to form your Intention for saying the Rosary, You might speak a six-syllable phrase:. "Now This is My Body." or "Touching Flesh With Spirit.", for example. Or anything else, as you say these first six beads, that takes you out of the ordinary world and into the particular exercise space of giving focused attention to your various body parts using a string of glass beads as a visual/tactile aid.

After the six-bead introduction, the Basic Rosary proper begins on the first lower Dark bead which represents the WHOLE RIGHT LEG. The sequence continues up the first six Dark beads to count the six Right Leg Chakras:

Whole Right Leg, Hip Joint, Thigh,

Knee, Calf, Ankle.

 

Continuing up the next six Dark beads to count the six Right Foot Chakras:

 

Five, Four, Three Toe,

Two, One Toe, Whole Right Foot. 

where here "One Toe" means the big toe. While saying each bead, direct your attention to the appropriate body part, physically touching it if you like, especially in the case of the toes, to isolate it from its nearby companions. Linger as long as seems appropriate on each chakra. Saying the Basic Rosary is not a race but a way of directing the gift of your attention to various otherwise neglected body parts.

After counting the 12 Right Leg:Foot Chakras, we move down the Rainbow beads to count the 8 classic Hindu Chakras, ordering them in Dark-Light pairs:

Ground, Crown,

Root, Brow,

Sex, Throat,

Belly, Heart.

where here I have located the four Dark Hindu chakras in the lower half of the body. Entire books have been written on Hindu chakra meditation so one can spend a lot of time if one is so inclined traversing just these eight Rainbow beads. In Nick's Basic Rosary the Rainbow beads are traversed from top to bottom without regard to their color. But in the Hindu chakra literature, the chakra colors are important and arranged in spectral sequence.

Now at the bottom of the Basic Rosary, we begin at the lower Light bead which represents the WHOLE RIGHT ARM. The sequence continues up the first six Light beads to count the six Right Arm Chakras:

Whole Right Arm, Shoulder Joint, Upper Arm,

Elbow, Forearm, Wrist.

Continuing up the next six Light beads to count the six Right Hand Chakras:

Five, Four, Three Finger,

Two, One Finger, Whole Right Hand.

where here "One Finger" means the thumb.

Saying the 12 Right Leg:Foot Chakras, the 8 Hindu Chakas, the 12 Right Arm:Hand Chakras demonstrates the principle of how to say the Basic Rosary and brings our chakra count to 32.

 

We see here how the 8 Hindu Chakras are "framed" by the 24 Right Limb Chakras. And our fingers are located now at the top of the rosary where Light, Dark and Rainbow come together.

We next go down the Rainbow path, counting the 8 Spinal chakras:

Will, Auto,

Neck, Tail,

Thorax, Pelvis,

Lumbar, Perineum.

where "Will" and "Auto" represent the voluntary and involuntary nervous systems located largely in nervous plexuses in the spine. The Will chakra you can actually engage with your mind; the dark Auto chakra is by definition unconscious but you can take this opportunity to appreciate and thank these loyal plexuses for their underground services. The Lumbar and Perineum are paired here because they are both saddle-shaped.

Next we count the 8 Portal Chakras, framing them like the Hindu Chakras with the 24 Left Limb Chakras:

 

Whole Left Leg, Hip Joint, Thigh, 

Knee, Calf, Ankle,

Five, Four, Three Toe,

Two, One Toe, Whole Left Foot.

Eyes, Ears,

Nose, Skin,

Mouth, Tongue,

Lungs, Bowels.

The Portal Chakras represent 8 ways the body connects to the outside world. The two-dot symbol representing the Nose/Skin chakra light/dark pair is meant to symbolize the Nose chakra by two nostrils and the Skin chakra by two armpits.

 

Whole Left Arm, Shoulder Joint, Upper Arm,

Elbow, Forearm, Wrist,

Five, Four, Three Finger,

Two, One Finger, Whole Left Hand.

This completes the counting of the 24 Central Chakras framed by the 48 Limb Chakras for a total of 72 chakras played out on the Basic 32-bead Chakra Rosary. What remains is only to count the chakras contained inside the 3 Bony Containers, then finish up with the Whole Body and No Body chakras.

Here is a chart summarizing where we have been and where we are going:

 

The Three Bony Containers consist of the Pelvic Basin, the Rib Cage and the Skull. The pelvic bones and the rib bones can be seen as mirror images of one another, so I make the pelvic bones "Dark" and the rib bones "Light".

 

The 8 Pelvic and 8 Rib Chakras are counted on the Rainbow beads starting at the top and counting down for the Pelvic Chakras, then reversing direction and counting up the Rainbow path for the Rib Chakras:

 

Whole Pelvic Basin, Sacrum,

Right Sitz Bone, Left Sitz Bone,

Right Pubic Bone, Left Pubic Bone,

Right Pelvic Bone, Left Pelvic Bone.

 

Right (lower) Rib, Left (lower) Rib,

Right Clavicle, Left Clavicle,

Right Scapula, Left Scapula,

Sternum, Whole Rib Cage.

(Note the nice homology between the pubic bones and the clavicles.) With these two Bony Containers we've added 16 more chakras to the rosary count. We now turn to our final Bony Container, the Skull.

For the eighteen Cranial Chakras we start at the top of the rosary and go down the Light path, formerly reserved for the Limb Chakras. Our count begins with the Temporomandibular Joints directly in front of the ears:

Right TM Joint, Left TM Joint,

Right Temporal Bone, Left Temporal Bone,

Right Occipital Bone, Left Occipital Bone,

Right Parietal Bone, Left Parietal Bone,

Right Frontal Bone, Left Frontal Bone,

Right Cheek Bone, Left Cheek Bone.

 

Counting these 12 chakra down the 12 Light beads takes us to the bottom of the rosary where we continue the count upwards along the Dark bead path

Chin Bone, Mandible,

Maxilla, Inion,

Foramen, Whole Skull.

 

Where the Inion is the prominent bump on the back of the skull and the Foramen is the hole in the bottom of the skull though which the spinal cord enters the brain.

 

Completing the Skull count with these last 6 chakras locates us in the middle of the Dark path, directly adjacent to the Dark Disk. 

Moving your fingers to the Dark Disk represents the Whole Body chakra. Hold the whole Basic Rosary dangling from this Dark Disk to bring your attention to the Whole Body signified by the dangling rosary.  Contemplate for a moment your whole body.

Then make the rosary disappear by dropping it into and closing your other hand. This gesture symbolizes the No Body chakra  -- the entire Universe minus that part you call your body. See how long and in what manner you can mentally inhabit this chakra -- everything in the world that is not you.

Experiencing the No Body chakra concludes the 108 chakra rosary.

Take from this exercise what you can. I hope you found it informative, amusing and not too complex.