 |
| August O'Connor, Celtic knot maker |
KAUFFMAN FLYPES ROLFSEN INTO O'CONNOR KNOT
My friend and musical partner, August O'Connor, designed me a personal Celtic knot which became part of my business card plus a rubber stamp, and which she also painted on my back, my bald head and on a hat box containing my black derby hat.
 |
| O'Connor knot painted on a hat box |
I recently discovered that knot theorists have classified knots according to the minimum number of their crossings and that the O'Connor knot is an example of a seven-crossing knot. According to the official knot table constructed by Dale Rolfsen there are only seven seven-crossing knots. So I naturally wondered which one of the seven Rolfsen knots corresponded to the O'Connor knot. After a simple but long and tedious calculation (presented in my previous post) I proved that the correct Rolfsen knot was 7--6.
In other words I had proved that it must be possible just by twisting and turning Rolfsen 7--6
 |
| The Rolfsen 7--6 knot |
to transform it into the O'Connor seven knot.
 |
| The O'Connor seven knot |
By tying a big rope in the shape of the Rolfsen knot and trying over and over again to turn it into an O'Connor knot (which I had proved must be possible) I ended up with nothing but featureless tangles and usually was unable to even return to the original Rolfsen. Then I had to untie the rope and try again.
In short, Nick could prove it but not do it.
For reasons unknown to me, Nick's dilemma attracted the attention of prominent knot theorist Louis Kauffman who demonstrated a simple set of three moves that easily turn Rolfsen into O'Connor.
 |
| Knot theorist Louis Kauffman |
Kauffman summarized his three moves on a single sheet of paper which I reproduce here. He also hinted that he might assign this exercise to his students as a homework problem.
 | |
| Kauffman's first move |
The O'Connor knot might be visualized as two outspread wings positioned over a "tail". Kauffman noticed that the O'Connor "tail" already occurs in the Rolfsen knot at 2 o'clock on the standard diagram, So Kauffman's first move is to rotate the Rolfsen till the "tail" is now at the bottom at 6 o'clock.
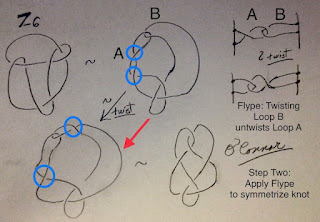 |
| Kauffman's second move |
For the second move we notice that the O'Connor knot's two "wings" are symmetric around the vertical axis but the Rolfsen knot is not. The Rolfsen knot has two crossings on the left-hand side (A) and zero crossings on the right (B), in the rotated sketch drawn by Kauffman.
For his second move, Kauffman then applies a twist that equalizes the number of crossings on the left and right hand sides. This twist (illustrated in the upper right corner of Kauffman's sketch) subtracts a crossing from one loop and adds it to the other. After this twist, technically called a "flype", both loops now contain the same number of crossings, and with a little bit of rearrangement, can be seen to resemble the "wings" of the O'Connor knot: Kauffman's third move.
 |
| Kauffman's third move |
Kauffman's first and third move are nothing but simple reaarrangements that can be accomplished without lifting the knotted rope from the table. The real trick resides in Kauffman's second move in which he applies a simple twist (called a flype) at precisely the right position. The word "flype" is derived from a Scottish word meaning to skin or fold as in turning over the edge of a sock.
Now I know how to turn a Rolfsen into an O'Connor knot. And so do you.
With grateful appreciation for Louis Kauffman's timely aid, I offer for your enjoyment the seemingly effortless liveliness of August O'Connor's "Knotted Hare"
 |
| August O'Connor's "Knotted Hare" |

